非对称加密

从一个故事开始：

我来翻译一下这个故事：

故事的主人公是 Bob，他有三个好朋友 Pat、Doug 和 Susan。
Bob 经常跟他们写信，因为他的信是明文传输的，在传递过程可能被人截获偷窥，
也可能被人截获然后又篡改了，更有可能别人伪装成 Bob 本人跟他的好朋友通信，
总之是不安全的。他很苦恼，经过一番苦苦探索，诶，他发现计算机安全学里有一种叫非对称加密算法的东东，
好像可以帮助他解决这个问题

说明：非对称加密算法（RSA）是内容加密的一类算法，
它有两个秘钥：公钥与私钥。公钥是公开的钥匙，所有人都可以知道，
私钥是保密的，只有持有者知道。通过公钥加密的内容，只能通过私钥解开。
非对称加密算法的安全性很高，但是因为计算量庞大，比较消耗性能。 好了，来看看 Bob 是怎么应用非对称加密算法与他的好朋友通信的： 1、首先 Bob 弄到了两把钥匙：公钥和私钥；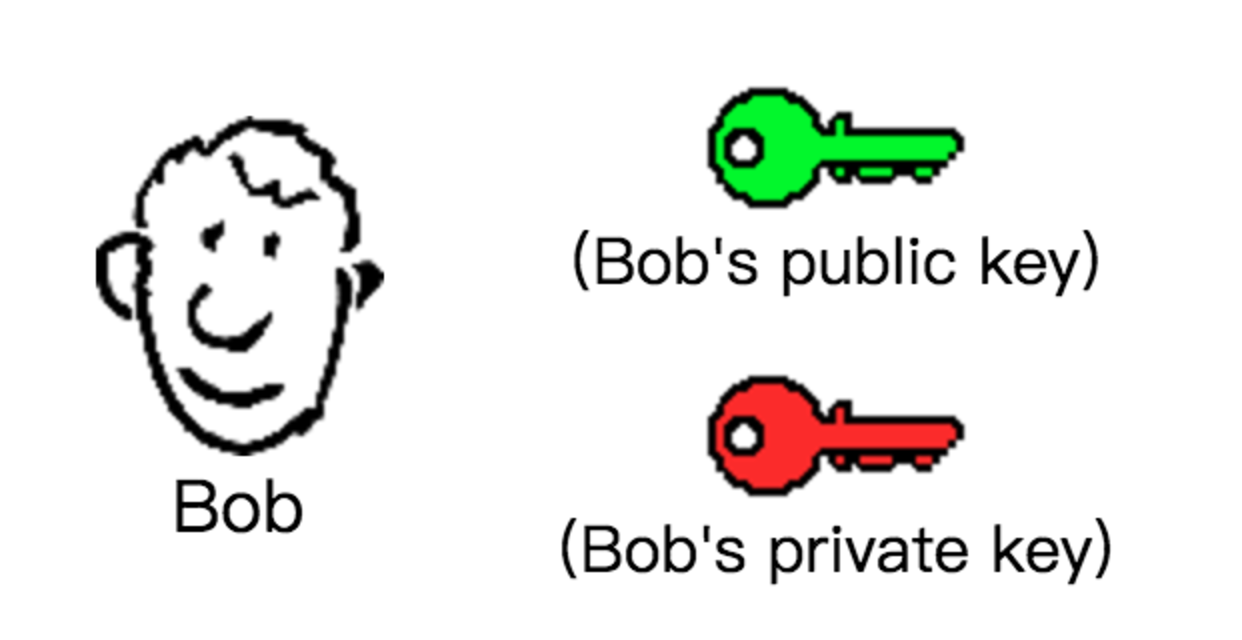

2、Bob 自己保留下了私钥，把公钥复制成三份送给了他的三个好朋友 Pat、Doug 和 Susan；

3、此时，Bob 总算可以安心地和他的好朋友愉快地通信了。
比如 Susan 要和他讨论关于去哪吃午饭的事情，
Susan 就可以先把自己的内容（明文）首先用 Bob 送给他的公钥做一次加密，然后把加密的内容传送给 Bob。
Bob 收到信后，再用自己的私钥解开信的内容；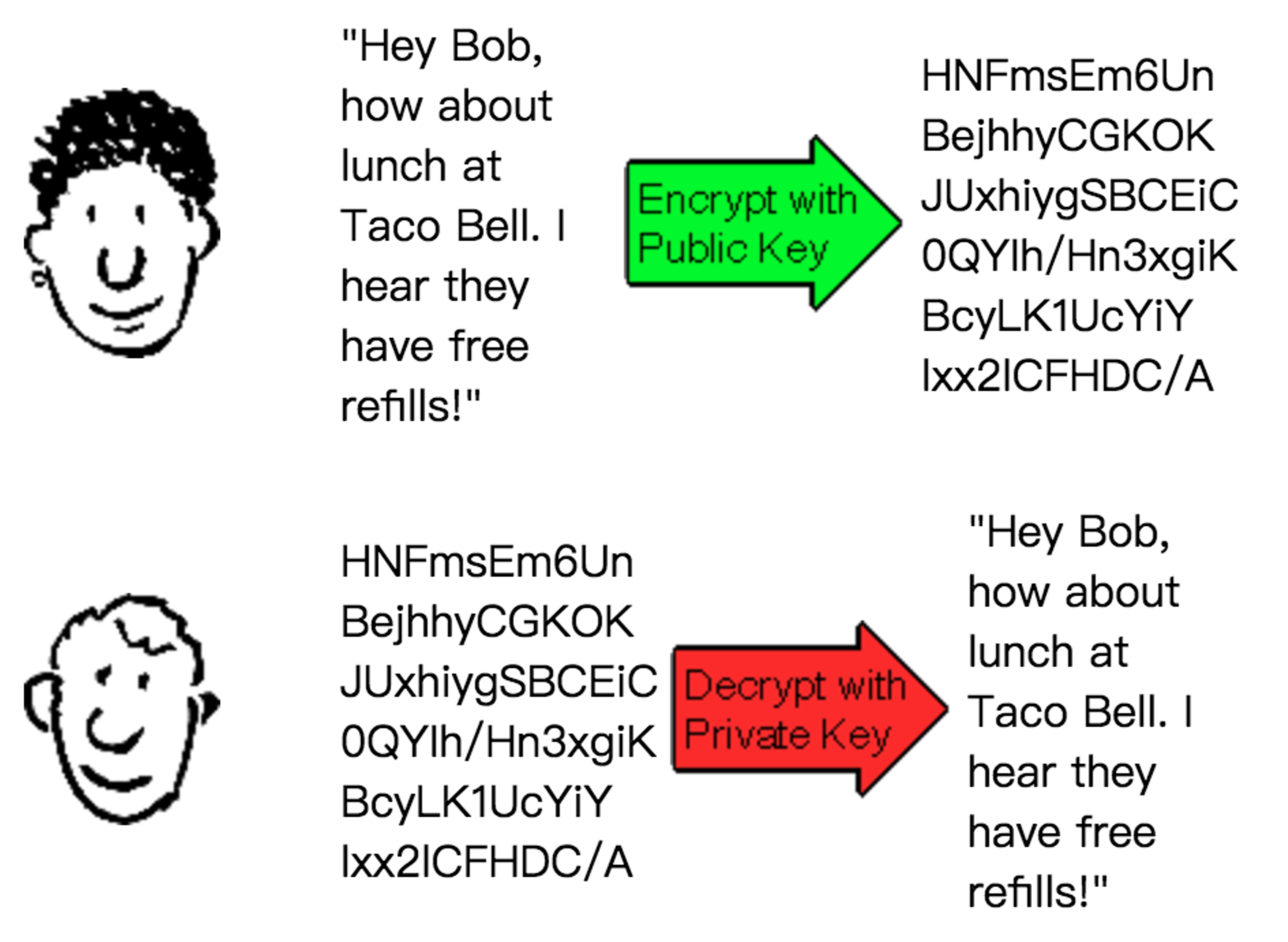

说明：这其实是计算机安全学里加密的概念，加密的目的是为了不让别人看到传送的内容，
加密的手段是通过一定的加密算法及约定的密钥进行的（比如上述用了非对称加密算法以及 Bob 的公钥），
而解密则需要相关的解密算法及约定的秘钥（如上述用了非对称加密算法和 Bob 自己的私钥），
可以看出加密是可逆的（可解密的）。

4、Bob 看完信后，决定给 Susan 回一封信。
为了防止信的内容被篡改（或者别人伪装成他的身份跟 Susan 通信），
他决定先对信的内容用 hash 算法做一次处理，得到一个字符串哈希值，
Bob 又用自己的私钥对哈希值做了一次加密得到一个签名，
然后把签名和信（明文的）一起发送给 Susan；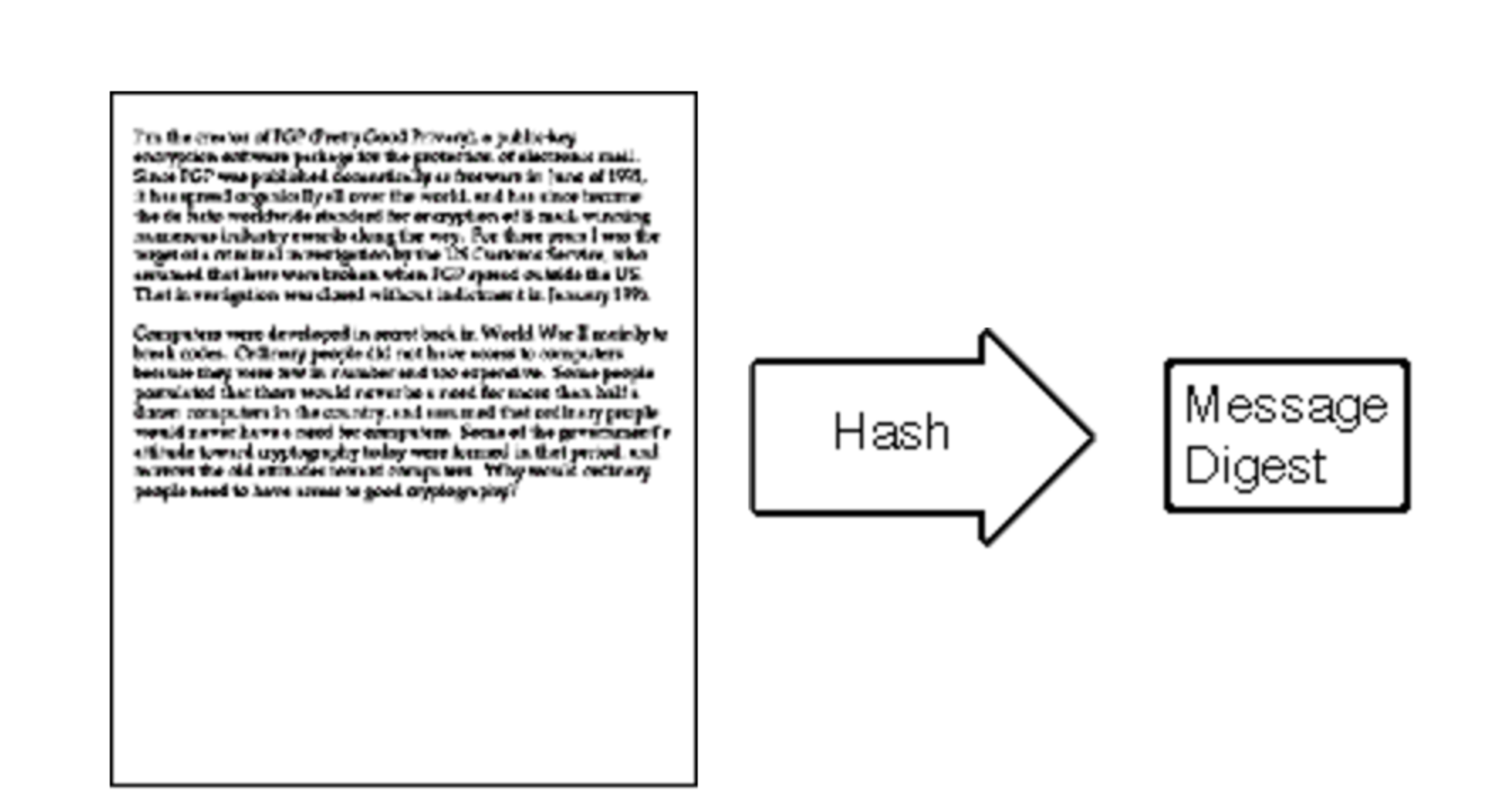



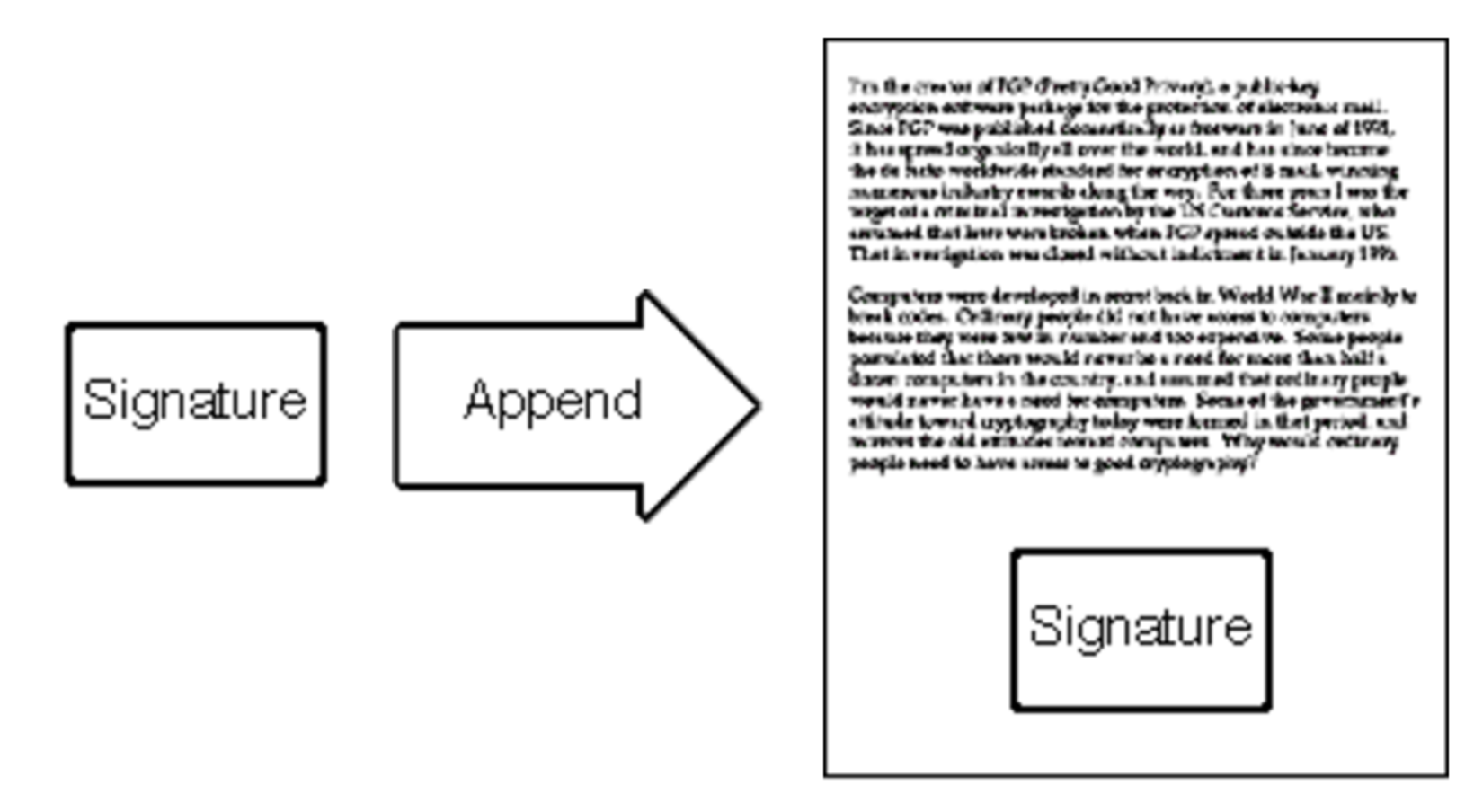
说明 2：Bob 的内容实质是明文传输的，所以这个过程是可以被人截获和窥探的，
但是 Bob 不担心被人窥探，他担心的是内容被人篡改或者有人冒充自己跟 Susan 通信。
这里其实涉及到了计算机安全学中的认证概念，Bob 要向 Susan 证明通信的对方是 Bob 本人，
另外也需要确保自己的内容是完整的。
5、Susan 接收到了 Bob 的信，首先用 Bob 给的公钥对签名作了解密处理，
得到了哈希值 A，然后 Susan 用了同样的 Hash 算法对信的内容作了一次哈希处理，
得到另外一个哈希值 B，对比 A 和 B，如果这两个值是相同的，那么可以确认信就是 Bob 本人写的，并且内容没有被篡改过；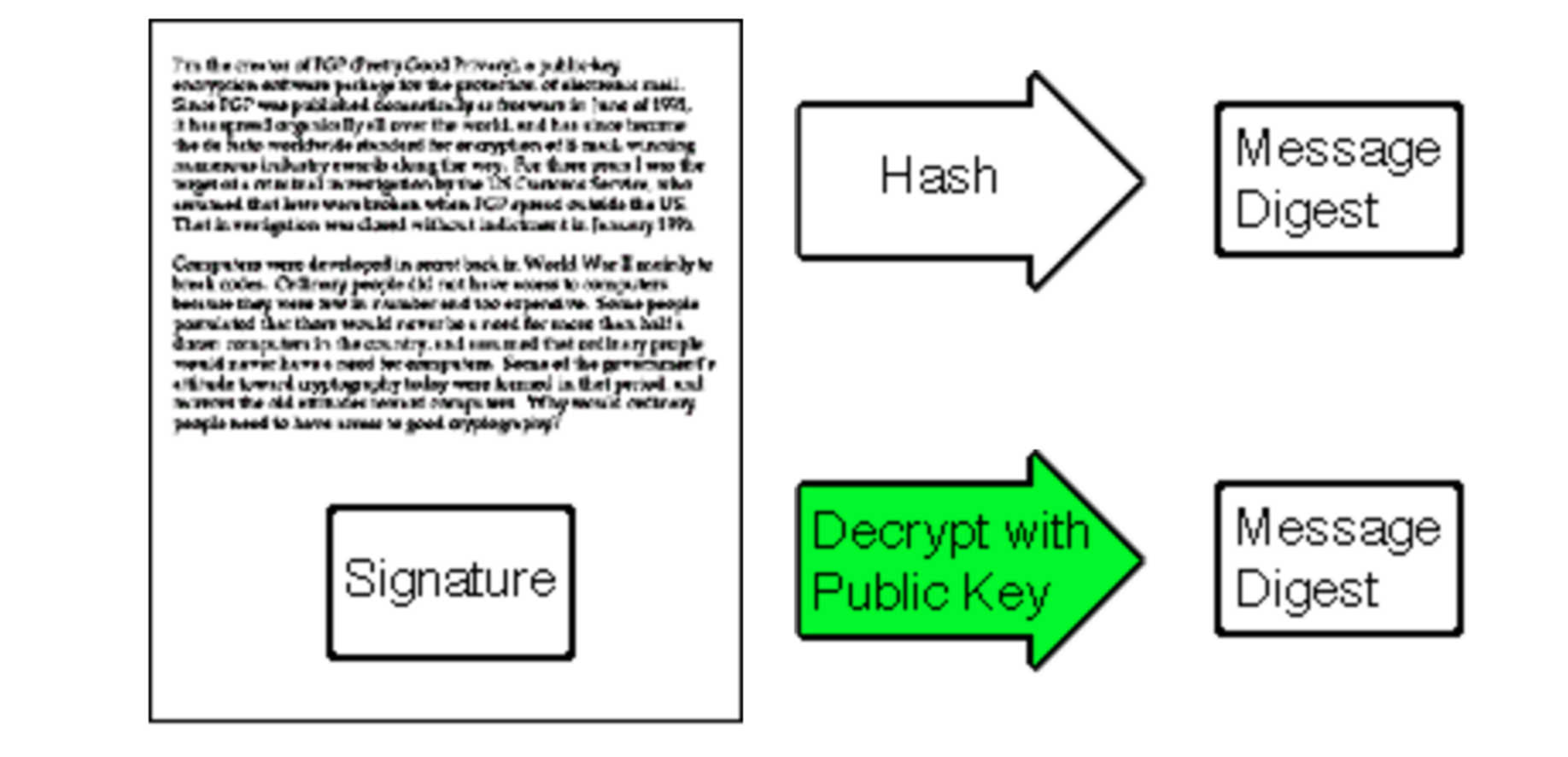

说明：4 跟 5 其实构成了一次完整的通过数字签名进行认证的过程。
数字签名的过程简述为：发送方通过不可逆算法对内容 text1 进行处理（哈希），
得到的结果值 hash1，然后用私钥加密 hash1 得到结果值 encry1。
对方接收 text1 和 encry1，用公钥解密 encry1 得到 hash1，
然后用 text1 进行同等的不可逆处理得到 hash2，对 hash1 和 hash2 进行对比即可认证发送方。
6、此时，另外一种比较复杂出现了，Bob 是通过网络把公钥寄送给他的三个好朋友的，
有一个不怀好意的家伙 Jerry 截获了 Bob 给 Doug 的公钥。
Jerry 开始伪装成 Bob 跟 Doug 通信，Doug 感觉通信的对象不像是 Bob，但是他又无法确认；

7、Bob 最终发现了自己的公钥被 Jerry 截获了，
他感觉自己的公钥通过网络传输给自己的小伙伴似乎也是不安全的，
不怀好意的家伙可以截获这个明文传输的公钥。
为此他想到了去第三方权威机构”证书中心”（certificate authority，简称 CA）做认证。
证书中心用自己的私钥对 Bob 的公钥和其它信息做了一次加密。
这样 Bob 通过网络将数字证书传递给他的小伙伴后，小伙伴们先用 CA 给的公钥解密证书，这样就可以安全获取 Bob 的公钥了。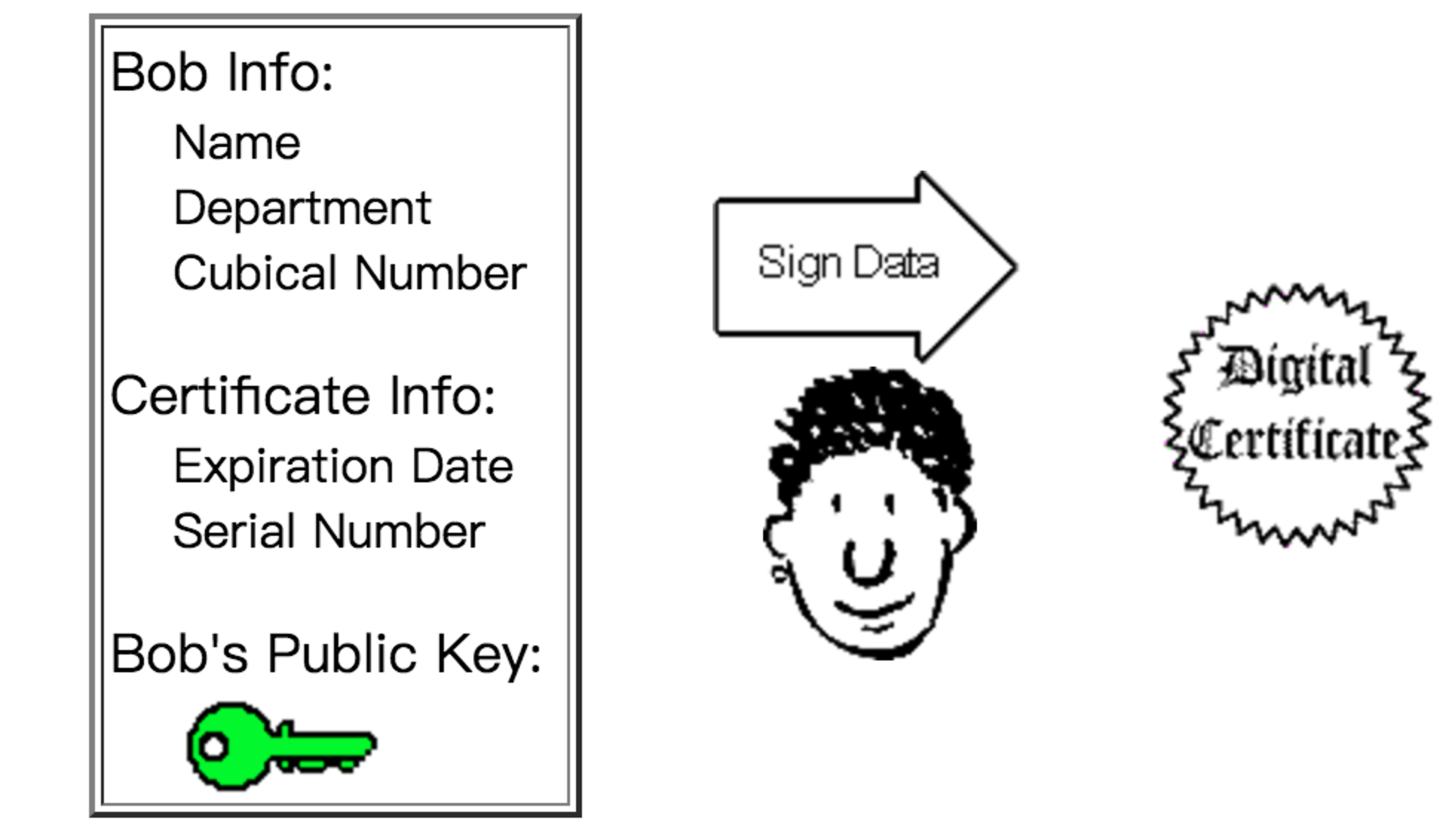

非对称加密容易误解的一个点–公钥和私钥到底哪个才是用来加密和哪个用来解密：

其中一个高赞回答：
不要去硬记。
你只要想：既然是加密，那肯定是不希望别人知道我的消息，所以只有我才能解密，所以可得出公钥负责加密，私钥负责解密；
同理，既然是签名，那肯定是不希望有人冒充我发消息，只有我才能发布这个签名，所以可得出私钥负责签名，公钥负责验证。

非对称加密的一个实现–RSA算法：

package rsa_algorithm

import (
	"bytes"
	"crypto/rand"
	"crypto/rsa"
	"crypto/x509"
	"encoding/pem"
	"errors"
)

func GenPair(bits int, passwd string) (priKey, pubKey []byte, err error) {
	// 生成私钥
	var privateKey *rsa.PrivateKey
	if privateKey, err = rsa.GenerateKey(rand.Reader, bits); err != nil {
		return
	}
	priStream := x509.MarshalPKCS1PrivateKey(privateKey)
	block := &pem.Block{Type: passwd, Bytes: priStream}
	priKey = pem.EncodeToMemory(block)
	// 生成公钥
	publicKey := &privateKey.PublicKey
	var pubStream []byte
	if pubStream, err = x509.MarshalPKIXPublicKey(publicKey); err != nil {
		return
	}
	block = &pem.Block{Type: passwd, Bytes: pubStream}
	pubKey = pem.EncodeToMemory(block)
	return
}

func Encrypt(pubKey, origData []byte) ([]byte, error) {
	block, _ := pem.Decode(pubKey)
	if block == nil {
		return nil, errors.New("public key error")
	}
	publicKey, err := x509.ParsePKIXPublicKey(block.Bytes)
	if err != nil {
		return nil, err
	}
	pub := publicKey.(*rsa.PublicKey)
	k := (pub.N.BitLen() + 7) / 8
	partLen := k - 11
	chunks := split(origData, partLen)
	buf := bytes.NewBuffer(make([]byte, 0, k))
	for _, chunk := range chunks {
		bytes, err := rsa.EncryptPKCS1v15(rand.Reader, pub, chunk)
		// fmt.Println("out chunk len:", len(bytes))
		if err != nil {
			return []byte{}, err
		}
		if _, err = buf.Write(bytes); err != nil {
			return []byte{}, err
		}
	}
	return buf.Bytes(), nil
}

func Decrypt(priKey, ciphertext []byte) ([]byte, error) {
	block, _ := pem.Decode(priKey)
	if block == nil {
		return nil, errors.New("private key error!")
	}
	privateKey, err := x509.ParsePKCS1PrivateKey(block.Bytes)
	if err != nil {
		return nil, err
	}
	partLen := (privateKey.N.BitLen() + 7) / 8
	chunks := split([]byte(ciphertext), partLen)
	buf := bytes.NewBuffer(make([]byte, 0, partLen))
	for _, chunk := range chunks {
		bytes, err := rsa.DecryptPKCS1v15(rand.Reader, privateKey, chunk)
		if err != nil {
			return []byte{}, err
		}
		if _, err = buf.Write(bytes); err != nil {
			return []byte{}, err
		}
	}
	return buf.Bytes(), nil
}

func split(buf []byte, lim int) [][]byte {
	var chunk []byte
	chunks := make([][]byte, 0, len(buf)/lim+1)
	for len(buf) >= lim {
		chunk, buf = buf[:lim], buf[lim:]
		chunks = append(chunks, chunk)
	}
	if len(buf) > 0 {
		chunks = append(chunks, buf)
	}
	return chunks
}

非对称加密的一个应用–https：

通过 Bob 与他的小伙伴的通信，我们已经可以大致了解一个安全通信的过程，
也可以了解基本的加密、解密、认证等概念。HTTPS 就是基于这样一个逻辑设计的。
首先看看组成 HTTPS 的协议：HTTP 协议和 SSL/TSL 协议。
HTTP 协议就不用讲了，而 SSL/TSL 就是负责加密解密等安全处理的模块，
所以 HTTPS 的核心在 SSL/TSL 上面。整个通信如下：

• 1、浏览器发起往服务器的 443 端口发起请求，请求携带了浏览器支持的加密算法和哈希算法。
• 2、服务器收到请求，选择浏览器支持的加密算法和哈希算法。
• 3、服务器下将数字证书返回给浏览器，这里的数字证书可以是向某个可靠机构申请的，也可以是自制的。
• 4、浏览器进入数字证书认证环节，这一部分是浏览器内置的 TSL 完成的：
  • 4.1 首先浏览器会从内置的证书列表中索引，找到服务器下发证书对应的机构，如果没有找到，此时就会提示用户该证书是不是由权威机构颁发，是不可信任的。如果查到了对应的机构，则取出该机构颁发的公钥.
  • 4.2 用机构的证书公钥解密得到证书的内容和证书签名，内容包括网站的网址、网站的公钥、证书的有效期等。浏览器会先验证证书签名的合法性（验证过程类似上面 Bob 和 Susan 的通信）。签名通过后，浏览器验证证书记录的网址是否和当前网址是一致的，不一致会提示用户。如果网址一致会检查证书有效期，证书过期了也会提示用户。这些都通过认证时，浏览器就可以安全使用证书中的网站公钥了。
  • 4.3 浏览器生成一个随机数 R，并使用网站公钥对 R 进行加密。
• 5、浏览器将加密的 R 传送给服务器。
• 6、服务器用自己的私钥解密得到 R。
• 7、服务器以 R 为密钥使用了对称加密算法加密网页内容并传输给浏览器。
• 8、浏览器以 R 为密钥使用之前约定好的解密算法获取网页内容。
  

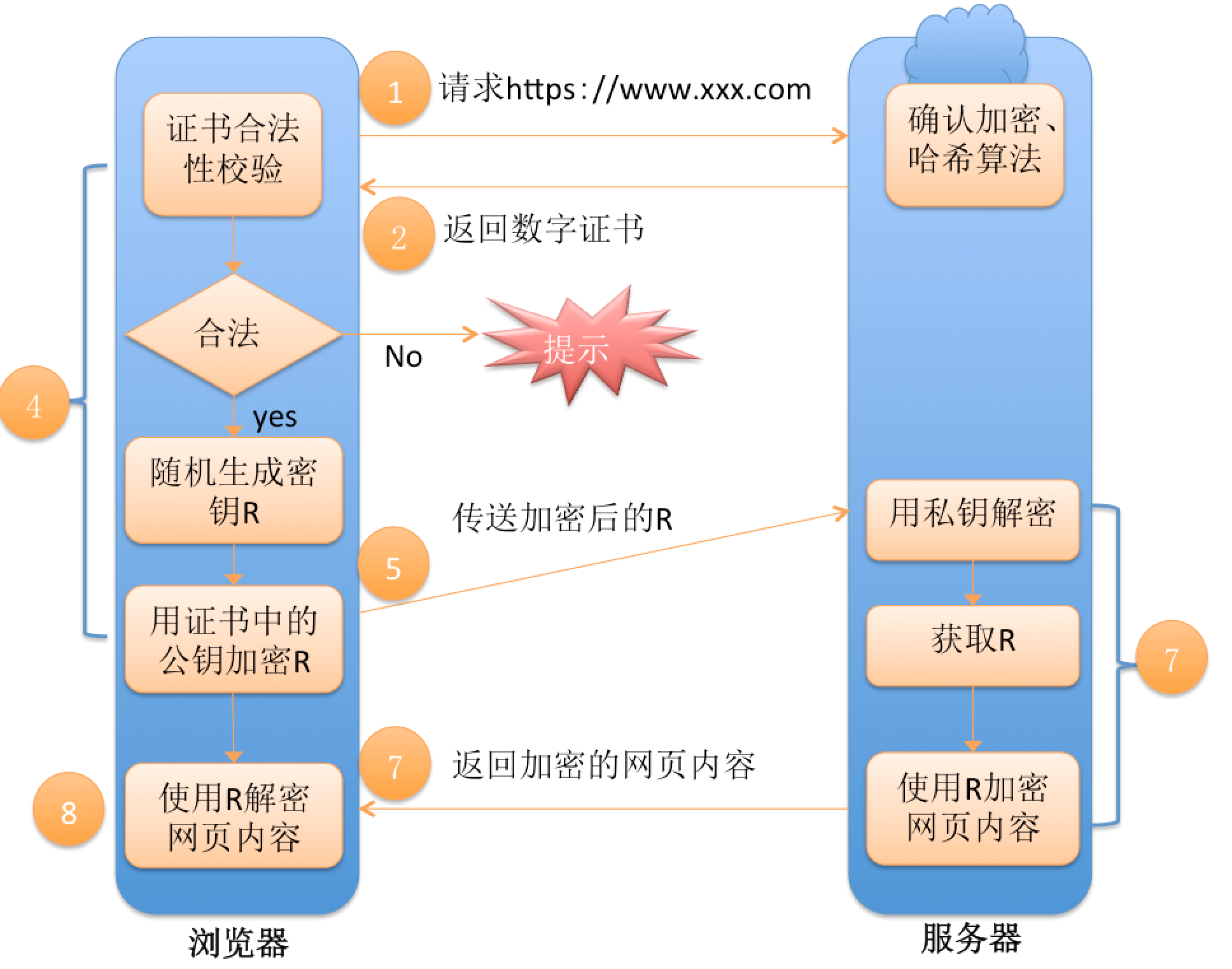
  备注 1：前 5 步其实就是 HTTPS 的握手过程，这个过程主要是认证服务端证书（内置的公钥）的合法性。
  因为非对称加密计算量较大，整个通信过程只会用到一次非对称加密算法（主要是用来保护传输客户端生成的用于对称加密的随机数私钥）。
  后续内容的加解密都是通过一开始约定好的对称加密算法进行的。

  备注 2：SSL/TLS 是 HTTPS 安全性的核心模块，TLS 的前身是 SSL，TLS1.0 就是 SSL3.1，
  TLS1.1 是 SSL3.2，TLS1.2 则是 SSL3.3。 SSL/TLS 是建立在 TCP 协议之上，因而也是应用层级别的协议。
  其包括 TLS Record Protocol 和 TLS Handshaking Protocols 两个模块，
  后者负责握手过程中的身份认证，前者则保证数据传输过程中的完整性和私密性